ちょっと間があきましたが、JOINのパフォーマンス関連の続きになります。
前回、JOINのパフォーマンスについての考察（リレーションとの関係）でJOINを行った結果、データが非正規化するとその非正規化の度合いによってパフォーマンスが下がるという話をしました。
前回の記事では、1対ｎの結合ではJOINを外す（単純なSQLに分割してホスト言語側で結合させる）ということで、定性的な話しかしていませんでしたが、幾つか実験を通して、もう少し定量的な話をしてみます。
『たかがJOINで、なぜこねくり回すのか？』と思われるかもしれませんが、こういう実験＆考察というのは意外に行われていないかと思います。私自身定性的なことは理解していたつもりでしたが、実際に実験を行うと色々と発見がありますので、記事にしてみます。
大切なことは解った気になることではなく真実を追究する姿勢で、先入観を持たずにきちんと実験を行いパフォーマンスに対する感性をみがくことは大切かと思います。
今回、調査するアルゴリズムについて
今まで何回か実験してきましたが、実験で使用してきたアルゴリズムについて説明します。１．SQLでJOINを行う。
SELECT Price.CODE, RDATE, OPEN, CLOSE, NAME FROM Price INNER JOIN Company ON (Price.CODE = Company.CODE)という風にSQLでJOINを行います。普通の処理になります。
２．ホスト言語側でJOINを行う（キャッシュ付のネステッドループJOINを行う）
１．のSQLを以下のように分割します。(1) SELECT CODE,RDATE,OPEN,CLOSE FROM Price (2) SELECT NAME FROM Company WHERE CODE = ?
(1)のSQLを実行して結果を取得しますが、NAMEについては(2)のように再度SQLを発行します。
ここで、単純にPriceテーブルの全ての行に対して(2)SQLを発行するのではなく同じ結果をキャッシュして同じCODEの場合はキャッシュからデータを取得するようにします。
３．ホスト言語側でJOINを行う（ハッシュJOINを行う）
１．のSQLを以下のように分割します。(１) SELECT CODE,NAME FROM Company (２) SELECT CODE,RDATE,OPEN,CLOSE FROM Price
（２）のPriceテーブルからのデータの取得に先立ちまして、（１）でComapnyテーブルから全てのデータを取得しておきます。
多くのDBMSで行っているハッシュ結合を真似ています。
1対ｎの2つのテーブルのJOINにおけるパフォーマンスモデル式
続いて、各アルゴリズムのパフォーマンス（実行時間）のモデル式を示します。ここで、
n ： Priceテーブルの行数
m ： Companyテーブルの行数
c10,c10,c20,c21,c22,c23,c30,c31,c32 ： 比例定数
になります。
１．SQLでJOINを行う
１．のパフォーマンスのモデル式は以下のようになります。c11 * n + c10
Priceテーブルの行数に比例した時間で結果を取得できます。ここでc11は比例定数であり、C10はオーバーヘッドにあたります。
２． ホスト言語側でJOINを行う（キャッシュ付のネステッドループJOINを行う）
２．のパフォーマンスのモデル式は以下のようになります。c21 * n + c22 * m + c20
Priceテーブルの行数に比例した時間と、Companyテーブルの行数に比例した時間およびオーバーヘッドの合計になります。
『c22 * m は c22 * n * m になるのでは？』と思われるかと思いますが、キャッシュのおかげでこのようになります。
また、「１．SQLでJOINを行う」と比べますと、c22 * m と余計な項が付いていますので、
SQLでJOINした方が速い
と早合点される方がいらっしゃるかと思いますが、JOINのパフォーマンスについての考察（リレーションとの関係）で述べたことは、c11とc22の定数値の差異となって現れてきます。
３．ホスト言語側でJOINを行う（ハッシュJOINを行う）
３．のパフォーマンスのモデル式は以下のようになります。c31 * n + c32 * m + c30
面白いことですが、形式的には「２． ホスト言語側でJOINを行う（キャッシュ付のネステッドループJOINを行う）」と同じになります。
ちなみに、[ADP開発日誌]SQL（JOIN）の実行パフォーマンスについて２０１１ にあります、「SQLの発行回数のオーバヘッドはどこにいったんや？」と思われるかもしれませんが、それはc32とc22の差異に出てくるということになります。
実験と結果
今回の実験では、nの値を変えながら実行時間を計測することにより、各モデル式の定数を求めます。求めるといってもグラフを書いて状況を観測します。厳密には回帰分析とかを行うことになるでしょうが、グラフが直線になることと、ｎが増えたときの傾向をつかめればよろしいかと思います。アルゴリズムの教科書ではオーダーという概念があり、オーダーでは定数を求めることは無意味とされています。つまり上記のアルゴリズムは論理的には違いがなくどれも一緒ということになります。
つまり、2倍や3倍の差はあまり意味がないということですが、もっとも、実際の現場ではこのような差にも敏感になるので、きちんと計測して値を出すことになります。
また、今回はｍは固定（約2000）で行っています。ｍが変動したときにどう変わるのかも興味深いですが今回は、m << n ということで結果にはあまり影響しません。
先ずは、結果から、
| 0行 | 373,740行 | 1,172,191行 | 2,002,749行 | 4,671,568行 | |
|---|---|---|---|---|---|
| １．SQLでJOIN | 718 | 10,015 | 29,938 | 52,329 | 119,192 |
| ２．キャッシュ付のネステッドループJOINを行う | 671 | 10,469 | 30,172 | 49,814 | 116,770 |
| ３．ハッシュJOINを行う | 2,828 | 11,422 | 29,797 | 49,845 | 110,988 |
つづいて、グラフを以下に示します。
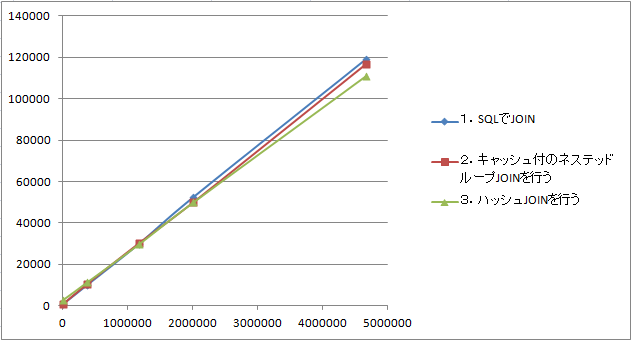
縦軸が時間で、横軸が行数（ｎ）になります。グラフをみますとPriceテーブルの行数（ｎ）が増えると「１．SQLでJOIN」より、「２．キャッシュ付のネステッドループJOINを行う」や「３．ハッシュJOINを行う」の方が速くなっていくことが解るかと思います。
パフォーマンスにシビアになる時は、往々にしてｎの行数が増えるような場合にあたるということになります。その場合は１より２や３を選択した方がよいということになります。
もっともグラフを見て解るとおり差はあまりないので、通常はやはり普通にSQLでJOINを行い、パフォーマンスを稼ぎたくなったら２や３を検討するということになるでしょう。